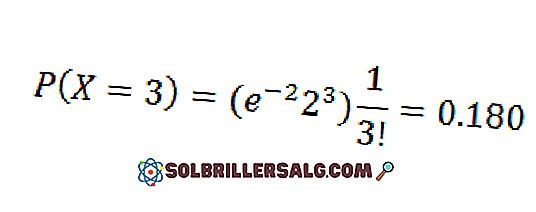Distribuzioni di probabilità discreta: caratteristiche ed esercizi
Le distribuzioni di probabilità discrete sono una funzione che assegna a ciascun elemento di X (S) = {x1, x2, ..., xi, ...}, dove X è una variabile casuale discreta data e S è il suo spazio campione, la probabilità che detto evento si verifica. Questa funzione f di X (S) definita come f (xi) = P (X = xi) è talvolta chiamata funzione di massa di probabilità.
Questa massa di probabilità viene solitamente rappresentata come una tabella. Poiché X è una variabile casuale discreta, X (S) ha un numero finito di eventi o un infinito numerabile. Tra le distribuzioni di probabilità discrete più comuni abbiamo la distribuzione uniforme, la distribuzione binomiale e la distribuzione di Poisson.

lineamenti
La funzione di distribuzione della probabilità deve soddisfare le seguenti condizioni:

Inoltre, se X prende solo un numero finito di valori (ad esempio x1, x2, ..., xn), quindi p (xi) = 0 se i> ny, quindi, la serie infinita di condizione b diventa un serie finita.
Questa funzione soddisfa anche le seguenti proprietà:
Sia B un evento associato alla variabile casuale X. Ciò significa che B è contenuto in X (S). In particolare, supponiamo che B = {xi1, xi2, ...}. pertanto:

In altre parole, la probabilità di un evento B è uguale alla somma delle probabilità dei singoli risultati associati a B.
Da ciò possiamo concludere che se a <b, gli eventi (X ≤ a) e (a <X ≤ b) si escludono a vicenda e, inoltre, la loro unione è l'evento (X ≤ b), quindi abbiamo:
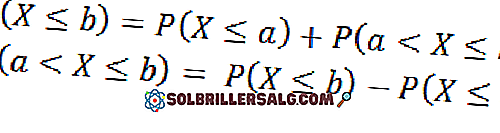
tipo
Distribuzione uniforme su n punti
Si dice che una variabile casuale X segue una distribuzione che è caratterizzata dall'essere uniforme in n punti se a ogni valore è assegnata la stessa probabilità. La sua funzione di massa di probabilità è:
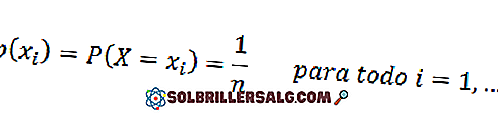
Supponiamo di avere un esperimento che ha due possibili risultati, può essere il lancio di una moneta i cui possibili risultati sono faccia o timbro, o la scelta di un numero intero il cui risultato può essere un numero pari o un numero dispari; Questo tipo di esperimento è noto come i test di Bernoulli.
In generale, i due possibili risultati sono chiamati successo e fallimento, dove p è la probabilità di successo e 1-p quella di fallimento. Possiamo determinare la probabilità di x successi in n test di Bernoulli indipendenti l'uno dall'altro con la seguente distribuzione.
Distribuzione binomiale
È quella funzione che rappresenta la probabilità di ottenere x successi in n test di Bernoulli indipendenti, la cui probabilità di successo è p. La sua funzione di massa di probabilità è:
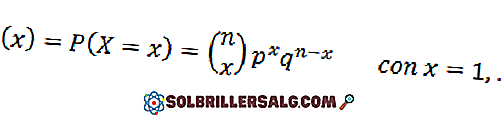
Il seguente grafico rappresenta la funzione di massa di probabilità per diversi valori dei parametri della distribuzione binomiale.

La seguente distribuzione deve il suo nome al matematico francese Simeon Poisson (1781-1840), che la ottenne come limite della distribuzione binomiale.
Distribuzione di Poisson
Si dice che una variabile casuale X abbia una distribuzione di Poisson del parametro λ quando può prendere i valori interi positivi 0, 1, 2, 3, ... con la seguente probabilità:

In questa espressione λ è il numero medio corrispondente alle occorrenze dell'evento per ogni unità di tempo, e x è il numero di volte in cui si verifica l'evento.
La sua funzione di massa di probabilità è:

Successivamente, un grafico che rappresenta la funzione di massa di probabilità per diversi valori dei parametri della distribuzione di Poisson.

Si noti che, finché il numero di successi è basso e il numero n di test eseguiti in una distribuzione binomiale è alto, possiamo sempre approssimare queste distribuzioni, poiché la distribuzione di Poisson è il limite della distribuzione binomiale.
La differenza principale tra queste due distribuzioni è che, mentre il binomio dipende da due parametri - vale a dire, n e p - l'unico di Poisson dipende da λ, che a volte viene chiamato l'intensità della distribuzione.
Finora abbiamo parlato solo di distribuzioni di probabilità per casi in cui i diversi esperimenti sono indipendenti l'uno dall'altro; cioè, quando il risultato di uno non è influenzato da qualche altro risultato.
Quando si verificano degli esperimenti che non sono indipendenti, la distribuzione ipergeometrica è molto utile.
Distribuzione ipergeometrica
Sia N il numero totale di oggetti di un insieme finito, di cui possiamo identificarne uno in qualche modo, formando un sottoinsieme K, il cui complemento è formato dagli elementi Nk rimanenti.
Se scegliamo casualmente n oggetti, la variabile casuale X che rappresenta il numero di oggetti appartenenti a K in quella elezione ha una distribuzione ipergeometrica dei parametri N, n e k. La sua funzione di massa di probabilità è:
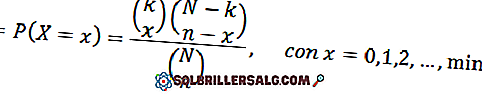
Il seguente grafico rappresenta la funzione di massa di probabilità per diversi valori dei parametri della distribuzione ipergeometrica.

Esercizi risolti
Primo esercizio
Supponiamo che la probabilità che un tubo radio (inserito in un determinato tipo di apparecchiatura) funzioni per più di 500 ore è 0, 2. Se vengono provate 20 provette, qual è la probabilità che esattamente k di queste funzioni più di 500 ore, k = 0, 1.2, ..., 20?
soluzione
Se X è il numero di tubi che funzionano più di 500 ore, assumeremo che X abbia una distribuzione binomiale. poi
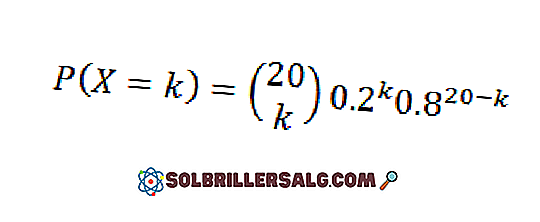
E così:

Per k≥11, le probabilità sono inferiori a 0, 001
Quindi possiamo vedere come la probabilità che questi k lavorino per più di 500 ore sale, fino a raggiungere il suo valore massimo (con k = 4) e poi inizia a diminuire.

Secondo esercizio
Una moneta viene lanciata 6 volte. Quando il risultato è costoso, diremo che è un successo. Qual è la probabilità che due facce emergano esattamente?
soluzione
Per questo caso abbiamo n = 6 e sia la probabilità di successo che di fallimento sono p = q = 1/2
Pertanto, la probabilità che vengano date due facce (cioè k = 2) è di
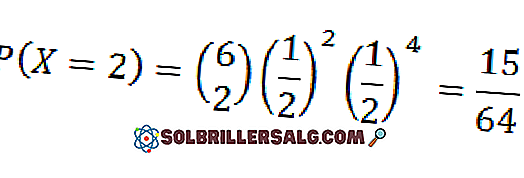
Terzo esercizio
Qual è la probabilità di trovare almeno quattro facce?
soluzione
Per questo caso abbiamo k = 4, 5 o 6
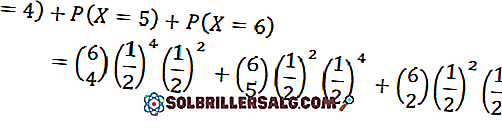
Terzo esercizio
Supponiamo che il 2% degli articoli prodotti in una fabbrica sia difettoso. Trova la probabilità P che ci siano tre articoli difettosi in un campione di 100 articoli.
soluzione
In questo caso potremmo applicare la distribuzione binomiale per n = 100 ep = 0.02, ottenendo come risultato:
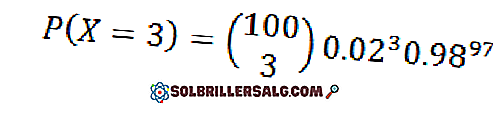
Tuttavia, poiché p è piccolo, usiamo l'approssimazione di Poisson con λ = np = 2. in tal modo,